7. The speckley Module

speckley is a high-order form of ripley, supporting structured, uniform meshes in two and three dimensions. Uniform meshes allow a more regular division of elements among compute nodes. Possible orders range from 2 to 10, inclusive.

speckley domains cannot be created by reading from a mesh file.

The family of domain that will result from a Rectangle or Brick call depends on which module is imported in the specific script. The following line is an example of importing speckley domains:

from esys.speckley import Rectangle, Brick

7.1. Formulation

For a single PDE that has a solution with a single component the linear PDE is defined in the following form:

()\[\int_{\Omega} D \cdot vu \; d\Omega + \int_{\Gamma} d \cdot vu \; d{\Gamma} = \int_{\Omega} X_{j} \cdot v_{,j}+ Y \cdot v \; d\Omega + \int_{\Gamma} y \cdot v \; d{\Gamma}\]

7.2. Meshes

speckley meshes are formed of regular elements using Gauss-Labatto-Legendre quadrature points. The number of quadrature points in each axis is dependent on the order of the domain. Examples of small Rectangle domains of different orders are shown in speckley_fig_meshes.

Meshfiles cannot be used to generate speckley domains.

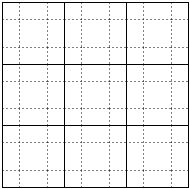
3x3 speckley Rectangle domain of order 3

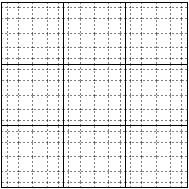
3x3 speckley Rectangle domain of order 6

3x3 speckley Rectangle domain of order 9

7.3. Linear Solvers in SolverOptions

While speckley has the same defaults as ripley, the HRZ_LUMPING must be set. PASO is not used in speckley.

7.4. Cross-domain Interpolation

Data on a speckley domain can be interpolated to a matching ripley domain provided the two domains have identical dimension, length, and, in multi-process situations, domain sub-divisions.

A utility class, SpeckleyToRipley is available to simplify meeting these conditions. To gain access to the class, the following will be required in the script:

from esys.escript.domainCouplers import SpeckleyToRipley

7.5. Functions

7.5.1. Brick

Brick(order, n0, n1, n2, l0=1., l1=1., l2=1., d0=-1, d1=-1, d2=-1, diracPoints=list(), diracTags=list())

Generates a Domain object representing a three-dimensional brick between \((0,0,0)\) and \((l0,l1,l2)\) with orthogonal faces. All elements will be regular and of order order. The brick is filled with:

• n0 elements along the \(x_0\)-axis

• n1 elements along the \(x_1\)-axis

• n2 elements along the \(x_2\)-axis

If built with MPI support, the domain will be subdivided:

• d0 times along the \(x_0\)-axis

• d1 times along the \(x_1\)-axis

• d2 times along the \(x_2\)-axis

d0, d1, and d2 must be factors of the number of MPI processes requested.

If axial subdivisions are not specified, automatic domain subdivision will take place. This may not be the most efficient construction and will likely result in extra elements being added to ensure proper distribution of work. Any extra elements added in this way will change the length of the domain proportionately.

diracPoints is a list of coordinate-tuples of points within the mesh, each point tagged with the respective string within diracTags.

7.5.2. Rectangle

Rectangle(order, n0, n1, l0=1., l1=1., d0=-1, d1=-1, diracPoints=list(), diracTags=list())

Generates a Domain object representing a two-dimensional rectangle between \((0,0)\) and \((l0,l1)\) with orthogonal faces. All elements will be regular and of order order. The rectangle is filled with:

• n0 elements along the \(x_0\)-axis

• n1 elements along the \(x_1\)-axis

If built with MPI support, the domain will be subdivided:

• d0 times along the \(x_0\)-axis

• d1 times along the \(x_1\)-axis

d0 and d1 must be factors of the number of MPI processes requested.

If axial subdivisions are not specified, automatic domain subdivision will take place. This may not be the most efficient construction and will likely result in extra elements being added to ensure proper distribution of work. Any extra elements added in this way will change the length of the domain proportionately.

diracPoints is a list of coordinate-tuples of points within the mesh, each point tagged with the respective string within diracTags.